Inhaltsverzeichnis
PG 573: MONET
Multi-Objective NETwork design: Implementierung und experimenteller Vergleich von Algorithmen zur mehrkriteriellen Optimierung von Netzwerk-Design-Problemen
Organisation
TeilnehmerInnen
- Jakob Bossek
- Michael Capelle
- Hendrik Fichtenberger
- Max Günther
- Johannes Kowald
- Marco Kuhnke
- David Mezlaf
- Christopher Morris
- Andreas Pauly
- Sven Selmke
- Sebastian Witte
Zeitraum
SoSe 2013, WiSe 2013/14
Umfang
jeweils 8 SWS im ersten und zweiten Semester, insgesamt 16 SWS
Veranstalter
eMail-Verteiler
- TeilnehmerInnen + Betreuer: pg573 *at* ls11.cs.tu-dortmund.de
- TeilnehmerInnen (ohne Betreuer): pg573s *at* ls11.cs.tu-dortmund.de
- nur Betreuer: pg573b *at* ls11.cs.tu-dortmund.de
Blockseminar
Zu Beginn der Projektgruppe steht ein Blockseminar. Nähere Informationen dazu sind hier zu finden.
Thema
In den letzten Wochen und Monaten war ein Thema in den Medien immer präsent:
der Netzausbau der Stromnetze in Deutschland.
Aufgrund der Energiewende und des vermehrten Einsatzes regenerativer Energien
muss das deutsche Stromnetz überarbeitet werden.
Ein Teil der bestehenden Trassen soll ausgebaut und darüber hinaus sollen neue Trassen errichtet werden.
In der nachfolgenden Abbildung ist ein Ausschnitt des aktuellen Stromnetzes mit einem
möglichen Ausbau zu sehen. Schwarze Flächen und Linien stehen für den bereits beschlossenen Ausbau
bis 2022.
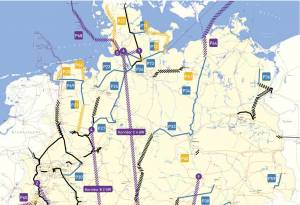
Die offizielle Planung des Aus- und Umbaus des Übertragungsnetzes erfolgt in 5 Phasen:
- Erstellung von Szenarien,
- Netzentwicklung und Umweltprüfung,
- Ermittlung des Bundesbedarfsplans,
- Planung der Trassenkorridore und
- Festlegung der konkreten Trassen.
In den ersten 4 Phasen werden zukünftige Bedarfe abgeschätzt, mögliche Trassenverläufe festgelegt und die Gebiete auf mögliche (negative) Folgen für Mensch, Tier und Umwelt überprüft.
Der letzte Schritt, insbesondere die auftretenden algorithmischen Probleme, sollen in dieser PG untersucht werden. Diese können als Netzwerk-Design- bzw. graphentheoretische Probleme formuliert werden: Eine neue Trasse bzw. ein Netzausbau entspricht in der einfachsten Form einem kürzesten Weg in einem gewichteten Graphen, wobei die Kantengewichte den Ausbaukosten entsprechen. Neben einfachen Wegen sind auch Teilbäume wie minimale Spannbäume von besonderem Interesse.
Zu den weiteren auftretenden Problemen, welche aus komplexitätstheoretischer Sicht schwieriger (NP-schwierig) sind, gehören die sogenannten Steinerbaumprobleme, bei denen nicht alle Knoten eines Graphen verbunden werden müssen.
Die genannten Probleme, ob NP-schwierig oder nicht, können in der Praxis mit bekannten Algorithmen effizient berechnet werden: für das Kürzeste-Wege-Problem liefert z.B. der Algorithmus von Dijkstra in polynomieller Zeit eine optimale Lösung. Der Algorithmus von Prim leistet dies für die Berechnung eines minimalen Spannbaumes. Für das Steinerbaumproblem sind ILP-Verfahren (Integer Linear Programming, ganzzahlige lineare Programmierung) wie Branch and Cut sehr erfolgreich.
Bei allen genannten Problemen und Algorithmen wird allerdings nur eine Zielfunktion optimiert, so dass typischerweise die Minimierung der Gesamtkosten im Vordergrund steht. Für das deutsche Stromnetz gibt es allerdings eine Reihe von wichtigen Faktoren und Zielen die ebenfalls optimiert werden sollen. So sind insbesondere die negativen Einflüsse auf die Umwelt zu minimieren und die neuen Trassen sollten nicht zu nah an bewohnte Gebiete heranreichen (und demnach der Protest der Bevölkerung nicht zu groß sein). Außerdem spielen physikalische Faktoren eine Rolle. Eine allein kostenminimale Lösung könnte z.B. durch ein Umweltschutzgebiet führen und somit von der eigentlich besten Lösung stark abweichen.
Eine weitere ähnliche Problemstellung stellt sich bei der Auswahl von Zugverbindungen: diese sollten möglichst wenig Zeit in Anspruch nehmen, günstig sein und wenige Umstiege enthalten.
 Mathematisch gesehen soll eine mehrkriterielle Zielfunktion optimiert werden.
In diesem Zusammenhang ist es nicht möglich von einem optimalen Lösungswert zu sprechen,
da z.B. für die bikriteriellen Wertevektoren
Mathematisch gesehen soll eine mehrkriterielle Zielfunktion optimiert werden.
In diesem Zusammenhang ist es nicht möglich von einem optimalen Lösungswert zu sprechen,
da z.B. für die bikriteriellen Wertevektoren 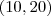 und
und 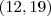 jeweils einer der Vektoren in einer Zielfunktion besser ist als der andere.
Es ist demnach bestenfalls möglich, eine Menge von nicht dominierten Vektoren zu finden.
Diese Menge wird auch Paretofront genannt.
Eine Lösung, deren Wertevektor nicht dominiert wird, heißt effizient; als Paretomenge wird die Menge der effizienten Lösungen bezeichnet.
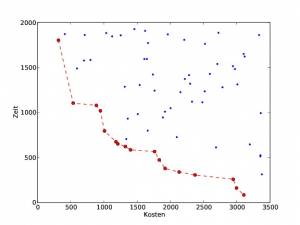
In der Regel ist das Ziel, alle oder eine repräsentative Teilmenge der effizienten Lösungen zu finden und dem Benutzer zu präsentieren, damit er auf der Grundlage dieser Daten eine Entscheidung fällen kann.
Die nebenstehende Abbildung zeigt exemplarisch das Bild einer zweidimensionalen Zielfunktion, wobei die Paretofront hervorgehoben ist.
jeweils einer der Vektoren in einer Zielfunktion besser ist als der andere.
Es ist demnach bestenfalls möglich, eine Menge von nicht dominierten Vektoren zu finden.
Diese Menge wird auch Paretofront genannt.
Eine Lösung, deren Wertevektor nicht dominiert wird, heißt effizient; als Paretomenge wird die Menge der effizienten Lösungen bezeichnet.
In der Regel ist das Ziel, alle oder eine repräsentative Teilmenge der effizienten Lösungen zu finden und dem Benutzer zu präsentieren, damit er auf der Grundlage dieser Daten eine Entscheidung fällen kann.
Die nebenstehende Abbildung zeigt exemplarisch das Bild einer zweidimensionalen Zielfunktion, wobei die Paretofront hervorgehoben ist.
Für die genannten Probleme existieren bereits einige Algorithmen, die die Menge der effizienten Lösungen vollständig aufzählen können – wenn man sich auf zwei Kriterien einschränkt. In beliebig vielen Kriterien gibt es für das Kürzeste-Wege-Problem ebenfalls eine Hand voll Algorithmen, wohingegen man für das mehrkriterielle Spannbaum-Problem bisher vergeblich suchen muss.
Die ersten Algorithmen waren Verfahren, die bereits bekannte Algorithmen für die einkriteriellen Varianten erweitern. Zu nennen wären beispielsweise die Algorithmen in [6] und [3], welche jeweils die bekannten Algorithmen von Dijkstra (Label Setting) und Bellman-Ford (Label Correcting) erweitern und mit beliebig vielen Zielfunktionen arbeiten. Für mehrkriterielle Spannbäume lässt sich ebenfalls der Algorithmus von Prim auf die mehrkriterielle Variante erweitern, um eine Teilmenge der effizienten Spannbäume zu finden, siehe z.B. [2].
Zudem gibt es spezifische Methoden aus der mehrkriteriellen Optimierung, die unterschiedlich erfolgreich angewendet werden. Eine Möglichkeit ist die Skalarisierung der Zielfunktion durch gewichtete Summen, sodass nur das klassische Problem mit einer Zielfunktion gelöst werden muss. Auch Meta-Heuristiken wie Evolutionäre Algorithmen finden häufige Verwendung.
Als dritte Säule werden speziell für die mehrkriterielle kombinatorische Optimierung neue Algorithmen entwickelt. Zu nennen ist beispielsweise die Two-Phases-Methode, die auf [12, 7] zurückgeht. Hier wird in einer ersten Phase eine leichter zu findende Teilmenge der effizienten Lösungen berechnet und in der zweiten Phase werden mit Hilfe dieser Lösungen die übrigen effizienten Lösungen aufgezählt. Sie ist ein vielversprechendes Verfahren, um mehrkriterielle Optimierungsprobleme zu lösen.
Aufgabenstellung
Aufgabe dieser Projektgruppe ist das Algorithm Engineering, d.h. die Entwicklung, Implementierung, theoretische Analyse und experimentelle Auswertung, von Algorithmen für mehrkriterielle Netzwerk-Design-Probleme. Primär sollen dabei das Kürzeste-Wege- und das Minimale-Spannbaum-Problem betrachtet werden. Weitere Probleme wie das Steinerbaumproblem wären aus Forschungssicht sehr interessant, sind aber optional.
Zur Lösung der Probleme können eigene Algorithmen entworfen oder bekannte Ansätze adaptiert werden. Unter den bekannten Ansätzen sind beispielsweise:
Für das Kürzeste-Wege-Problem:
- [1] (bikriteriell, Ranking),
- [7] (bikriteriell, Two-Phases-Methode),
- [9] (bikriteriell, Label Correcting),
- [6] (
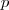 -kriteriell, Label Setting),
-kriteriell, Label Setting), - [3] (
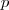 -kriteriell, Label Correcting).
-kriteriell, Label Correcting).
Zur Berechnung effizienter Spannbäume:
- [10] (bikriteriell, Two-Phases-Methode),
- [8] (bikriteriell, Two-Phases-Methode),
- [5] (bikriteriell, Two-Phases-Methode),
- [2] (
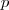 -kriteriell, Prim),
-kriteriell, Prim), - [13] (
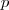 -kriteriell, Evolutionäre Algorithmen).
-kriteriell, Evolutionäre Algorithmen).
Um die Algorithmen testen zu können, soll zusätzlich eine Experimentierplattform implementiert werden. Diese kann als GUI (Graphical User Interface) oder CLI (Command Line Interface) umgesetzt werden. Das Interface soll die Auswahl an zu testenden Algorithmen, Parametereingaben, Instanzen und Auswertungswerkzeugen ermöglichen. Die Plattform ist modular zu gestalten, sodass leicht neue Algorithmen, Instanzen und Auswertungswerkzeuge auch für andere Probleme hinzugefügt werden können. Im Anschluss an die Experimente sollen die Ergebnisse ausgegeben und gespeichert werden; dies soll in Form von grafisch ansprechenden Diagrammen geschehen.
Im Zuge der Implementierung muss der Quellcode dokumentiert werden. Als Programmiersprache können C++, Java, oder/und Python eingesetzt werden. Die notwendige Entscheidung für die Programmiersprache fällt die Projektgruppe in den ersten Wochen selbst.
Anforderungen
Teilnahmevoraussetzungen
- Erfahrung in C++, Java oder Python
- Vorkenntnisse in Graphenalgorithmen, mehrkriterieller Optimierung oder effizienten Algorithmen bzw. Datenstrukturen
- Optional: Kentnisse in den Bereichen Softwarekonstruktion und Algorithm Engineering
Minimalziele
- Design und Implementierung einer modularen Experimentierplattform für die betrachteten Graphenalgorithmen
- mehrkriterielle Kürzeste-Wege-Probleme und effiziente Spannbäume:
- Entwicklung, Implementierung und Analyse von jeweils mindestens drei Algorithmen
- Experimentelle Auswertung der Algorithmen anhand von praxisnahen Instanzen des Netzausbaus mit Hilfe der Experimentierplatform
- Dokumentation, Zwischen-/Abschlussbericht, Präsentationen der Ergebnisse
Literatur
- A bicriterion shortest path algorithm
J.C.M. Climaco, E.Q.V. Martins
European Journal of Operational Research, 11:399–404, 1982 - Efficient spanning trees
H.W. Corley
Journal of Optimization Theory and Applications, 45(3):481–485, 1985 - Shortest paths in networks with vector weights
H.W. Corley, I.D. Moon
Journal of Optimization Theory and Applications, 46(1):79–86, 1985 - A discussion of scalarization techniques for multiple objective integer programming
M. Ehrgott
Annals of Operations Research, 147(1):343–360, 2006 - On spanning tree problems with multiple objectives
H.W. Hamacher, G. Ruhe
Annals of Operations Research, 52:209–230, 1994 - On a multicriteria shortest path problem
E.Q.V. Martins
European Journal of Operational Research, 16:236–245, 1984 - A parametric approach to solving bicriterion shortest path problems
J. Mote, I. Murthy, D.L. Olson
European Journal of Operational Research, 53:81–92, 1991 - The problem of the optimal biobjective spanning tree
R.M. Ramos, S. Alonso, J. Sicillia, C. Gonzales
European Journal of Operational Research, 111:617–628, 1998 - A label correcting approach for solving bicriterion shortest-path problems
A.J.V. Skriver, K.A. Andersen
Computers & Operations Research, 27:507–524, 2000 - Solving the biobjective minimum spanning tree problem using a k-best algorithm
S. Steiner, T. Radzik
Technischer Bericht TR-03-06, King's College London, 2003 - A multicriteria Pareto-optimal path algorithm
C.T. Tung, K.L. Chew
European Journal of Operational Research, 62:203–209, 1992 - The two-phases method: An efficient procedure to solve bi-objective combinatorial optimization problems
E.L. Ulungu, J. Teghem
Foundations of Computing and Decision Sciences, 20(2):149–165, 1995 - Genetic algorithm approach on multi-criteria minimum spanning tree problem
G. Zhou, M. Gen
European Journal of Operational Research, 114:141–152, 1999

